 |
|
 |
 |
 |
Testes Intermédios /Exames
|
 |
 |
 |
|
 |
 |
|
 |
|
 |
|
 |
 |
 |
Matemáticos / Problemas / Curiosidades
|
 |
 |
 |
A forma pitagórica de calcular potências com expoente 2 - 23 de abril de 2019
O número mágico - 3 de janeiro de 2019
Raízes de números quadrados perfeitos - 24 de outubro de 2018
Área do círculo - 3.º Período - 4 de abril de 2016 Área do círculo
A área do círculo é dada por 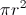 , onde 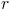 é o raio do círculo. Ao dividir-se o círculo em setores circulares iguais e subdividindo-os em setores circulares cada vez menores em ângulo e, consequentemente, em área, até ao infinito, podemos agrupá-los por forma a obtermos um retângulo de comprimento 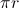 e largura 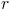 . A área do retângulo é dada pelo produto do comprimento pela largura, obtendo-se assim o valor 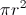 .
Triângulo de Penrose - 2.º Período - 4 de janeiro de 2016 Triângulo de Penrose
O triângulo de Penrose é um objeto impossível. Apesar do seu nome, foi o artista sueco Oscar Reutersvärd que criou-o em . No entanto, foi o matemático inglês Roger Penrose quem concebeu-o de forma independente e popularizou-o na década de , descrevendo-o como "a impossibilidade em sua forma mais pura".
No GIF animado acima podemos ver uma esfera a percorrer o triângulo de Penrose. A continuidade do movimento da esfera sobre o triângulo também é impossível, uma vez que uma representação em 3D do objeto obriga a haver uma ruptura, que apenas não é visível de um determinado ângulo.
Teorema de Pitágoras - 1.ºPeríodo - 30 de setembro de 2015Teorema de Pitágoras

O Teorema de Pitágoras refere que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. No GIF animado podemos visualizar o Teorema de Pitágoras de uma forma intuitiva. No entanto, não se trata de uma demonstração e sim de uma aplicação do mesmo teorema utilizando os volumes dos prismas quadrangulares retos.
3D - 7 de abril de 2015Parabolóide hiperbólico
É uma superfície em 3D gerada pela equação algébrica 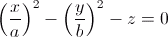 , onde 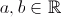 .
Algumas batatas fritas são um exemplo de um parabolóide hiperbólico. Esta forma, permite ao snack ser firmemente empilhado num recipiente cilíndrico evitando a quebra durante o empacotamento e o transporte.
3D - 5 de janeiro de 2015Toro

Em Geometria, o Toro é, em linguagem popular, um objeto cuja forma é um donut. Mais precisamente, o Toro é um sólido de revolução gerado pela rotação de um círculo de raio num espaço tridimensional em torno de um eixo coplanar à uma distância do seu centro.
A forma do toro depende do sinal da expressão :
- R = 0: O toro é uma esfera, pois o eixo de rotação é um dos diâmetros do círculo;
- R < r: O toro diz-se "cruzado" e toma a forma de uma abóbora;
- R = r: O toro diz-se "colar sem abertura";
- R > r: O toro diz-se "aberto" e assemelha-se à um donut.
A equação algébrica de um toro é da forma 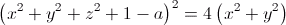 em que 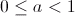
3D - 16 de outubro de 2014Tira de Moebius
A tira de Moebius é uma superfície que possui apenas um lado e com uma componente de fronteira. Ela tem a propriedade matemática de ser não orientável. A tira de Moebius foi descoberta independentemente pelos matemáticos alemães August Ferdinand Möbius e Johann Benedict Listing em .
Pode-se realizar um modelo em papel de forma simples: recortando uma tira, fazendo uma meia-volta à tira e colam-se as extremidades, dando a sua forma característica.
A tira de Moebius possui várias propriedades curiosas. Cortando a tira longitudinalmente e ao meio desta, aparece uma outra tira (não é uma tira de Moebius porque tem duas faces) mas com o dobro do comprimento da original. Cortando a tira longitudinalmente e com um terço da sua largura, obtemos duas tiras encaixadas, sendo uma mais pequena que a outra. A menor é uma tira de Moebius e a maior não.
A tira de Moebius possui muitas aplicações, nomeadamente na arquitetura, design e engenharia.
Estádio Aviva (Dublin - Irlanda)
Ponte Moebius (Bristol - Inglaterra)
Carro Moebius (Tommaso Gecchelin - segundo prémio do International Car Design Contest 2010)
A equação algébrica para a tira de Moebius clássica de grau é:
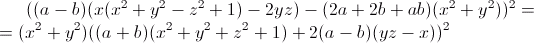
A vida de um Matemático... - 16 de junho de 2011Paolo Ruffini
 Paolo Ruffini, médico e matemático, nasceu em Valentano, Papal States (Itália) em 22 de Setembro de 1765, e morreu no dia 10 de Maio de 1822 em Modena (agora Itália). No princípio pretendeu entrar em Ordens Santas e chegou a receber a tonsure, mas mudou de ideias e começou a estudar Matemática e Medicina na Universidade de Modena onde recebeu o grau de doutor. Aos vinte e três anos foi designado professor de Análise depois de ter substituído durante um ano o seu professor Cassiani. Em 1791, lecciona a cadeira de Matemática Elementar. Enquanto isso, não negligenciou o estudo e prática da Medicina. No tempo da invasão francesa em Itália (1796), foi inesperadamente designado membro do Juniori no corpo legislativo de Milan. Continuo a ter sucesso quando voltou às suas conferências em Modena. Por ter recusado levar o juramento republicano sem a declaração condicional ditada pela sua consciência, foi despedido da sua posição como um conferencista público. Mas com o retorno dos austríacos em 1799 foi restabelecido ao seu posto anterior e mantido lá pelos governos seguintes. Paolo Ruffini, médico e matemático, nasceu em Valentano, Papal States (Itália) em 22 de Setembro de 1765, e morreu no dia 10 de Maio de 1822 em Modena (agora Itália). No princípio pretendeu entrar em Ordens Santas e chegou a receber a tonsure, mas mudou de ideias e começou a estudar Matemática e Medicina na Universidade de Modena onde recebeu o grau de doutor. Aos vinte e três anos foi designado professor de Análise depois de ter substituído durante um ano o seu professor Cassiani. Em 1791, lecciona a cadeira de Matemática Elementar. Enquanto isso, não negligenciou o estudo e prática da Medicina. No tempo da invasão francesa em Itália (1796), foi inesperadamente designado membro do Juniori no corpo legislativo de Milan. Continuo a ter sucesso quando voltou às suas conferências em Modena. Por ter recusado levar o juramento republicano sem a declaração condicional ditada pela sua consciência, foi despedido da sua posição como um conferencista público. Mas com o retorno dos austríacos em 1799 foi restabelecido ao seu posto anterior e mantido lá pelos governos seguintes.
Ruffini recusou leccionar a mais importante cadeira de matemática em Pavia, porque não queria deixar a prática da medicina. Em 1806 aceitou leccionar a cadeira de Matemática Aplicada na escola militar recentemente estabelecida. Em 1814 Franceso IV restabeleceu a universidade e designou Ruffini reitor para a vida, e ao mesmo tempo professor de Medicina Prática e Matemática Aplicada. Pelas suas conferências com os pacientes da época, reavivou os estudos clínicos que tinham sido abandonados durante vários anos. Durante a epidemia de tifo de 1817 sacrificou-se pelos seus concidadãos, e finalmente sucumbiu. Foi enterrado na Igreja de Santa Maria di Pomposa, entre os túmulos de Sigonio e Muratori.
Palavras Cruzadas...Matemáticas - 16 de junho de 2011
VERTICAIS
1 - As equações têm sempre um; juntar; quinhentos; inicial de trigonometria.
2 - Um; mil; quociente da divisão da soma de várias quantidades pelo número destas.
3 - Conjunto de números onde aparecem os intervalos; mil; elemento absorvente da multiplicação.
4 - Soma de dois números simétricos; quinhentos; sólido geométrico que não tem qualquer superfície plana; segmento de recta com origem no ponto A e extremidade no ponto B.
5 - Intervalo; negação (princípio); elemento conhecido que serve de base à resolução de um problema; conjunto dos números reais.
6 - Aplicação; dois.
7 - Quantificador universal (contrário); coeficiente genérico; negação; sólido geométrico com seis faces iguais.
8 - Superfície limitada por duas circunferências concêntricas; números inteiros relativos e naturais; nulo; dez.
9 - Quantificador de existência (contrário); quantificador universal (contrário); números reais; intersecção de duas faces de um sólido geométrico.
10 - O seu símbolo é uma chaveta; inicial de intersecção; inicial de gráfico; contém.
11 - Quadrilátero que contém os pontos A, N, O, R; reais; dez; quadrado de zero.
12 - Pertence; primeiro; polígono de 20 lados (princípio); coeficiente nulo; reunião; inicial de trapézio.
13 - Polígono de quatro lados iguais (princípio); intersecção de duas rectas; elemento do contradomínio da função (princípio).
HORIZONTAIS
1 - Um; figuras planas que limitam um sólido geométrico.
2 - Ângulo de 360º; reunião; o mesmo que raiz de um polinómio; condição que exprime a desigualdade entre duas expressões designatórias (princípio).
3 - Intersecção (ao contrário); pertence; conjunto dos números naturais; ângulo de 180º; reunião.
4 - Inicial de ângulo; soma; polígono de três lados (princípio).
5 - Cinquenta; inicial de irracional; quantificador universal (ao contrário); superfície de uma figura plana.
6 - Razão entre a medida do comprimento do cateto oposto e da hipotenusa do triângulo rectângulo; um milhar; razão entre o comprimento da circunferência e o seu raio (ao contrário).
7 - Qualquer potência de expoente nulo; princípio de seno; porção de circunferência compreendida entre dois pontos.
8 - Variável natural; falso; números naturais e inteiros relativos; raio de extremidade N.
9 - Primeiro; segmento de recta que une um vértice do triângulo com o meio do lado oposto; segmento de recta com origem em S e extremidade em T.
10 - Inicial de radiano; segmento de recta que une o centro da circunferência com qualquer dos seus pontos; radical (inicial); nulo.
11 - Potência de base 10 e expoente três; adicionar (princípio); recta na qual se considera, um ponto O, chamado origem, que a divide em duas semi-rectas uma positiva e outra negativa.
12 - Raiz quadrada de cem; primeiro elemento do conjunto dos números naturais; razão entre a medida de comprimento do cateto adjacente e da hipotenusa do triângulo rectângulo; elemento neutro da multiplicação.
13 - Dezena (princípio); reunião; razão entre a medida de comprimento do cateto oposto e do cateto adjacente do triângulo rectângulo; fracção de termos iguais.
14 - Desembaraçar; área do rectângulo; inicial de abcissa.
15 - Ângulo de lados OA e OB; elemento neutro da adição; razão entre a medida de comprimento do cateto adjacente e o cateto oposto do triângulo rectângulo.
Problema mês de Maio - 6 de junho de 2011A Beatriz, o Pedro e o Bruno foram colher maças. A Beatriz colheu três vezes mais do que o Pedro e o Bruno colheu mais quatro do que os outros dois em conjunto. No total colheram 212 maças.

Quantas maças colheram cada um?”

Solução
x = n.º maças colhidas pelo Pedro
3x = n.º de maças colhidas pela Beatriz
x + 3x + 4 = n.º de maças colhidas pelo Bruno
N.º total de maças = 212
Logo,
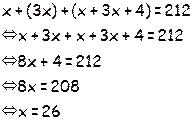
O Pedro colheu 26 maças, a Beatriz colheu três vezes mais, ou seja, 78 maças e o Bruno colheu as restantes 108 maças.
Curiosidade mês Maio - 6 de junho de 2011Os caracteres numéricos que usamos hoje têm uma origem árabe (provavelmente marroquina) e têm mais de mil anos. Uma possível explicação histórica é a de que a erosão provocada pelo uso alterou-os ligeiramente, mas a idéia original parece ter uma explicação curiosa:
O "1" tem um ângulo
O "2" tem dois ângulos
O "3" tem três ângulos
O "0" tem zero ângulos!
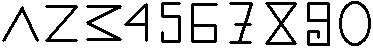
A vida de um Matemático... - 6 de junho de 2011
Maurits Cornelis Escher (1898-19720) nasceu na Holanda, mais precisamente em Leeuwarden. Depois do secundário pensou seguir arquitectura, mas o conhecimento travado com Samuel de Mesquita guiou-o na direcção do Desenho. Canhoto, tal como Miguel Ângelo e Leonardo da Vinci, especializou-se no desenho de espaços impossíveis e na criação de ilusões de óptica através do uso da perspectiva, divisão regular do plano, geometria hiperbólica e topologia. Escher não tinha grande treino matemático, no entanto trocou correspondência com matemáticos, como os ingleses Harold Scott MacDonald Coxeter e Roger Penrose, de forma a aperfeiçoar o seu trabalho.
As obras de M.C.Escher, o artista gráfico que muitos dizem ter alma de matemático, continuam a apaixonar o mundo.
Problema do mês de Abril - 28 de abril de 2011O testamento do tio Ambrósio
O tio Ambrósio deixou em testamento, aos seus três sobrinhos, um terreno com 1419 metros quadrados.

O testamento dizia:
"O Nicolau ficará com mais 54 metros quadrados do que o Jaime; o Jaime ficará com mais 39 metros quadrados do que a Rita".
Os sobrinhos, embora intrigados com a decisão do tio, cumpriram o testamento.
Com quantos metros quadrados ficou cada um?
Solução

Curiosidade do mês de Abril - 28 de abril de 2011Corda de 13 nós
Os antigos egípcios usavam uma corda com 13 nós igualmente espaçados para determinar um ângulo recto e, do mesmo modo, determinar a perpendicular a uma dada recta.

A corda de 13 nós igualmente espaçados ficava dividida em 12 partes iguais.
Um homem A segurava os dois nós extremos (o 1º e o 13º); um segundo homem, B, segurava o 4.º nó; e um terceiro homem, C, segurava o 8.º nó.
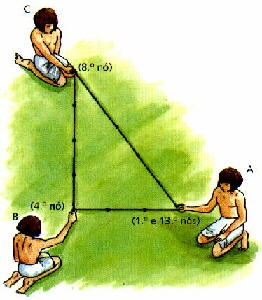
Afastavam-se, então, de forma a que a corda entre eles ficasse bem esticada.
Quando isso acontecia, tinha-se formado um triângulo rectângulo e, consequentemente, também um ângulo recto.
Para determinar a perpendicular a uma recta r, bastaria que os homens A e B se colocassem sobre r. Neste caso, a recta definida pela corda segurada pelos homens B e C dá a perpendicular a r.
Efectivamente esta técnica permite construir um triângulo cujos lados medem 3 e 5, referidas à unidade de comprimento definida por dois nós consecutivos.
Ora, estas medidas verificam o teorema de Pitágoras.
Com efeito 32+42 =52, ou seja, 9+16=25. E como o teorema de Pitágoras diz respeito a triângulos rectângulos, é de admitir que este triângulo seja rectângulo, onde o ângulo recto se opõe ao lado de medida 5 (hipotenusa).
Estes conhecimentos permitiam resolver certo tipo de problemas práticos tais como o das marcações das propriedades do antigo Egipto que as cheias do Nilo modificavam e faziam desaparecer todos os anos.
A vida de um Matemático... - 28 de abril de 2011
Arquimedes
(287 a.c. - 212 a.c.)
Arquimedes nasceu (julga-se) no ano 287 a.C. em Siracusa - actual Sicília. Foi educado em Alexandria, no actual Egipto e pensa-se que terá sido aluno de Euclides. Alexandria era naquela época o grande centro do saber e Euclides um dos maiores matemáticos.
Depois de voltar à sua terra natal, Arquimedes fez inúmeras investigações e descobertas nas áreas da Matemática, Mecânica e Hidrostática.
Na Matemática, Arquimedes foi capaz de determinar o valor de pi, encontrou a relação entre a superfície e o volume de uma esfera, estudou as propriedades da parábola e utilizou o método da exaustão para calcular áreas, por exemplo.
Na Mecânica, inventou a ?Balança de Arquimedes?, descobriu o princípio da alavanca simples e das roldanas; inventou a roldana composta. É de Arquimedes a célebre frase:
Dêem-me um ponto de apoio e moverei a Terra!
Arquimedes foi igualmente um grande inventor de máquinas de guerra, como catapultas e um sistema de espelhos para incendiar barcos inimigos.
Inventou ainda o parafuso de Arquimedes, muito útil para elevar água. Na Hidrostática, descobriu a Lei da Impulsão, ou Princípio de Arquimedes, com a sua célebre experiência da banheira!
Durante a 2.ª Guerra Púnica, as tropas romanas comandadas pelo general Marcelo, cercaram Siracusa. Graças às máquinas de guerra inventadas por Arquimedes, conseguiram aguentar o cerco durante dois anos, mantendo os romanos fora da ilha.
Conta-se que quando os romanos invadiram a ilha, Arquimedes se encontrava na praia desenhando na areia, a estudar problemas de geometria. Um soldado romano ordenou-lhe que o acompanhasse a casa do general Marcelo. Arquimedes continuou a sua tarefa, ignorando a ordem do soldado romano. Perante a desobediência, o soldado romano irritou-se e matou-o ali mesmo na praia.
A vida de uma Matemática... - 29 de março de 2011 Hipátia (370- 415) Hipátia (370- 415)
Entre os génios matemáticos da Antiguidade conta-se Hipátia, a primeira grande matemática de que se tem conhecimento.
Hipátia era filha de Teão de Alexandria e irmã de Epifânio, grandes matemáticos da época.
A sua educação foi acompanhada de perto pelo seu pai, e incluía treino físico diário, arte, ciência, literatura e filosofia. A oratória e a retórica, com grande importância na aceitação e integração das pessoas na sociedade da época, também não foram deixadas ao acaso. No campo religioso, recebeu informação sobre todos os sistemas de religião conhecidos, tendo o seu pai assegurado que nenhuma religião ou crença lhe limitaria a busca e a construção do seu próprio conhecimento.
Hipátia depressa eclipsou o irmão, devido ao seu saber, gentileza, palavra, talento e beleza. Em Alexandria estudou geometria e astronomia, partindo depois para Atenas com o objectivo de aumentar os seus conhecimentos. Quando regressou a Alexandria foi convidada para dar aulas no Museu, juntamente com aqueles que haviam sido seus professores. A sua paixão pela matemática e a sua inteligência brilhante reflectiam-se nas suas aulas que atraíam estudantes de várias partes do mundo.
Do seu trabalho, pouco chegou até nós. Alguns tratados foram destruídos com a Biblioteca, outros perderam-se quando o templo de Serápis foi saqueado.
A tragédia de Hipátia foi ter vivido numa época de luta entre o paganismo e o cristianismo. Sendo ela uma ilustre pagã, em 415, a ira dos cristãos abateu-se sobre ela. Quando regressava do Museu, foi assaltada em plena rua e lapidada. Posteriormente o seu corpo foi lacerado com conchas de ostra, e ou cacos de cerâmica, consoante as versões existentes. Os seus membros ensanguentados foram simplesmente exibidos pelas ruas...
Problema do mês de Março - 29 de março de 2011Tesouro
O pirata que desenhou o mapa escreveu uma pista falsa, de modo a que não se descobrisse a ilha onde escondeu o tesouro. Mesmo assim, tenta descobri-la.
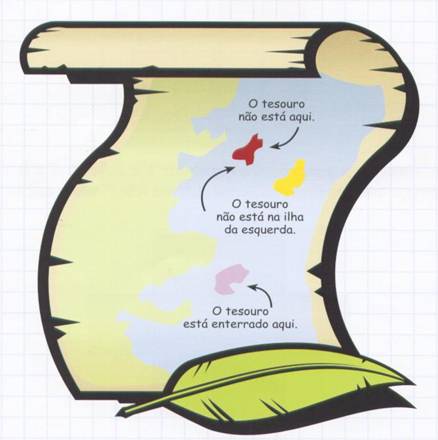
Solução
A pista “O tesouro está enterrado aqui” é falsa. Por isso o tesouro só pode estar na ilha cuja pista é “O tesouro não está na ilha da esquerda”.
Curiosidade do mês de Março - 29 de março de 2011 3,14159265358979323846 3,14159265358979323846
Este é apenas o início de um número muito especial com uma infinidade de casas decimais: o número p - a razão entre o perímetro de um círculo e o seu diâmetro.
No dia 14 de Março (data que nos EUA se escreve 3/14), celebra-se em todo o mundo o Dia do p (3,14.). Esta celebração tem como objectivo promover junto do público em geral o gosto pela matemática, aproveitando o interesse que o p tem suscitado ao longo dos tempos em todas as culturas.
O ano de 2006 é muito especial, porque marca o 300º aniversário da aplicação da letra grega p para designar este número, utilizada pela primeira vez em 1706 na publicação "Synopsis Palmariorium Mathesios" de William Jones.
Problema do mês de Fevereiro - 21 de fevereiro de 2011 Alice no país das dúvidas...

Solução
Se o caminho fosse o 1, teríamos as placas 1 e 2 correctas, o que contraria o enunciado. Se o caminho fosse o 3, novamente teríamos 2 placas correctas, a 2 e a 3. Portanto, o caminho certo é o 2 e a única placa verdadeira é a 3.
A Vida de um Matemático... - 21 de fevereiro de 2011Leonhard Euler

A contribuição de Euler para a matemática teve como um de seus pilares a Introductio in analysim infinitorum (1748; Introdução à análise dos infinitos), obra que constitui um dos fundamentos da matemática moderna.
Leonhard Euler nasceu na cidade suíça de Basileia em 15 de Abril de 1707, numa família tradicionalmente dedicada à pesquisa científica. A precocidade e o brilhantismo de seus primeiros trabalhos despertaram o interesse dos principais matemáticos de sua época, como Jean Bernouilli e seus filhos, e converteram-no, aos vinte anos, em membro associado da Academia de Ciências de São Petersburgo, para onde se transferira. Por meio de livros e monografias que apresentou à Academia, Euler aperfeiçoou os conhecimentos da época sobre cálculo integral, desenvolveu a teoria das funções trigonométrica e logarítmica e simplificou as operações relacionadas à análise matemática. A sua contribuição para a geometria analítica e para a trigonometria é comparável à de Euclides para a geometria plana. A tendência a expressar operações físicas e matemáticas em termos aritméticos incorporou-se desde então aos procedimentos das ciências exatas.
Em consequência de um problema neurológico, Euler perdeu em 1735 a visão de um olho. Chamado em 1741 por Frederico II o Grande, da Prússia, foi honrado com a dignidade de membro da Academia de Berlim.
Ao perder o favor real, em 1766, transferiu-se de novo para a corte de São Petersburgo, a cujo trono havia subido Catarina II a Grande, e ali estendeu a sua actividade ao estudo da mecânica, óptica, acústica e astrofísica. Estudou o movimento lunar, o fenómeno dos eclipses e as posições relativas dos astros.
As principais descobertas de Euler deram-se no campo da teoria dos números. Euler também foi responsável pela incorporação de numerosos símbolos à linguagem matemática, como para designar somatório; e para denominar a base dos logaritmos naturais ou neperianos e a, b, e c para os lados de um triângulo e A, B e C para seus ângulos. Euler não esmoreceu a sua actividade nem mesmo quando ficou cego, aos sessenta anos. Morreu em 18 de Setembro de 1783, em São Petersburgo.
Assinatura de Euler:
Curiosidade - 21 de fevereiro de 2011
Vê o que acontece se multiplicarmos 37 por Múltiplos de 3.

Curioso, não achas?
A vida de um Matemático... - 12 de janeiro de 2011Euclides

Euclides (c. 330 a. C. - 260 a. C.) nasceu na Síria e estudou em Atenas. Foi um dos primeiros geómetras e é reconhecido como um dos matemáticos mais importantes da Grécia Clássica e de todos os tempos.
Muito pouco se sabe da sua vida. Sabe-se que foi chamado para ensinar Matemática na escola criada por Ptolomeu Soter (306 a. C. - 283 a. C.), em Alexandria, mais conhecida por "Museu". Aí alcançou grande prestígio pela forma brilhante como ensinava Geometria e Álgebra, conseguindo atrair para as suas lições um grande número de discípulos. Diz-se que tinha grande capacidade e habilidade de exposição e algumas lendas caracterizam-no como um bondoso velho.
Conta-se que, um dia, o rei lhe perguntou se não existia um método mais simples para aprender geometria e que Euclides respondeu: "Não existem estradas reais para se chegar à geometria".
Outro episódio sobre Euclides refere-se a um dos seus discípulos, o qual, resolvendo ser espirituoso, depois de aprender a primeira proposição de geometria lhe perguntou qual o lucro que lhe poderia advir do estudo da geometria. Nesse momento, Euclides - para quem a geometria era coisa séria - chamou um escravo, passou-lhe algumas moedas e ordenou que as entregasse ao aluno: "já que deve obter um lucro de tudo o que aprende".
Euclides é exemplo do "Puro Homem da Ciência", que se dedica à especulação pelo gosto do saber, independentemente das suas aplicações materiais.
Embora se tenham perdido mais de metade dos seus livros, ainda restaram, para felicidade dos séculos vindouros, os treze famosos livros que constituem os Elementos. Publicados por volta de 300 a. C., aí está contemplada a aritmética, a geometria e a álgebra.
Muitos outros textos lhe são atribuídos, dos quais se conhecem alguns títulos:
- Divisões de superfícies,
- Data ( continha aplicações da álgebra à geometria numa linguagem estritamente geométrica),
- Pseudaria,
- Tratado sobre Harmonia,
- A Divisão (continha muito provavelmente 36 proposições relativas à divisão de configurações planas),
- Os Dados (formavam um manual de tabelas, servindo como guia de resolução de problemas, com relação entre medidas lineares e angulares num círculo dado),
- Óptica (seria um estudo da perspectiva e desenvolveria uma teoria contrária à de Aristóteles, segundo a qual é o olho que envia os raios que vão até ao objecto que vemos e não o inverso).
- Os fenómenos (celestes) (pensa-se que Euclides discorreria sobre Geometria esférica para utilização dos astrónomos),
- Porismos (um dos mais lamentáveis desaparecimentos, este livro poderia conter aproximações à Geometria Analítica).
O trabalho de Euclides é tão vasto que alguns historiadores não acreditavam que fosse obra de um só homem. Os trabalhos matemáticos que chegaram até nós foram inicialmente traduzidos para árabe, depois para latim, e a partir destes dois idiomas para outras línguas europeias.
Embora alguns conceitos já fossem conhecidos anteriormente à sua época, o que impossibilita uma análise completa da sua originalidade, pode-se considerar o seu trabalho genial. Ao recolher tudo o que então se conhecia, sistematiza os dados da intuição e substitui imagens concretas por noções abstractas, para poder raciocinar sem qualquer apoio intuitivo.
Resolução do problema do mês de Dezembro - 12 de janeiro de 2011
Curiosidade - 12 de janeiro de 2011O que é um Número Capicua?

Um número Capicua é um número que se lê do mesmo modo da esquerda para a direita ou da direita para a esquerda.
Por exemplo 77, 434, 6446, 82328.
Para obteres um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua.
Exemplo:
Partindo do número 84 ,
84 + 48 = 132;
132 + 231 = 363, que é um Número Capicua.
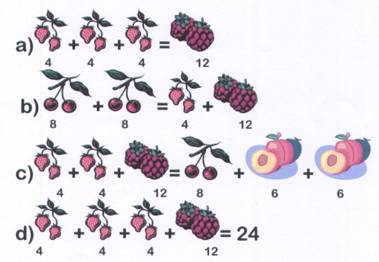
Problema do mês de Janeiro - 12 de janeiro de 2011Salada de fruta
Descobre o valor de cada fruto nas somas seguintes:
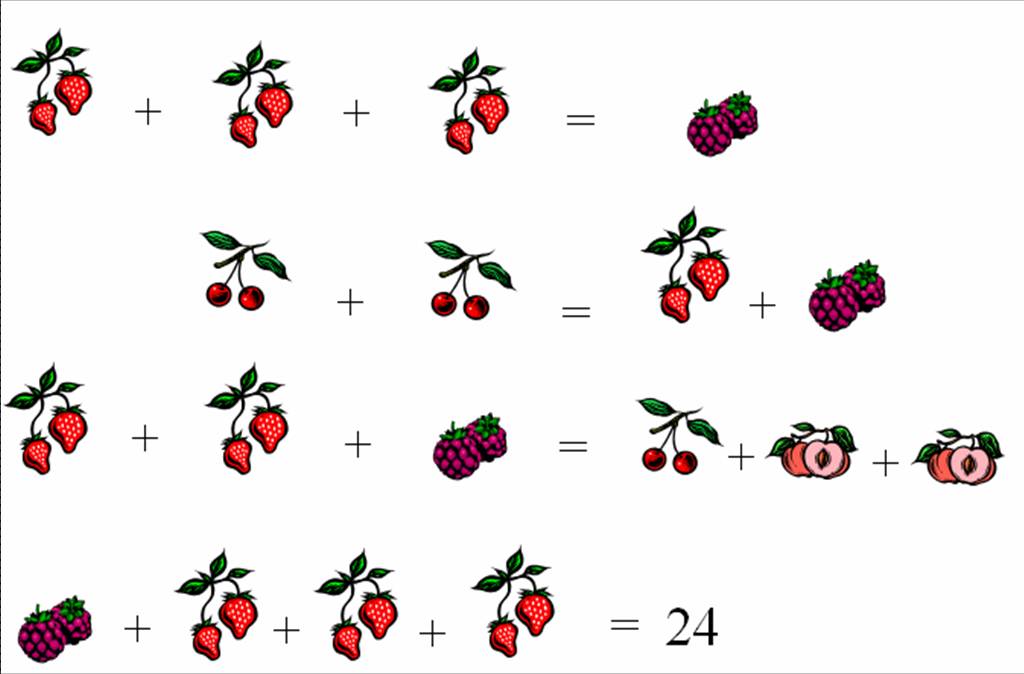
Solução
Solução do problema do mês de Novembro - 6 de dezembro de 2010R: Devem passar primeiro Carlos e Romerito (2 m). Volta Romerito com a lanterna (3 m). Passam Camila e Manolito (11 m). Volta Carlos com a lanterna (13 m). Por último cruzam de novo Carlos e Romerito (15 minutos).
Curiosidade - 6 de dezembro de 2010
Número mágico
1089 é conhecido como o número mágico
Veja porquê:
Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297+972=1089 número mágico
A vida de um Matemático - 6 de dezembro de 2010Pitágoras

Pitágoras foi um importante matemático e filósofo grego. Nasceu no ano de 570 a .C na ilha de Samos, na região da Ásia Menor (Magna Grécia). Provavelmente, morreu em 497 ou 496 a.c em Metaponto (região sul da Itália). Embora sua biografia seja marcada por diversas lendas e factos não comprovados pela História, temos dados e informações importantes sobre sua vida. Com 18 anos de idade, Pitágoras já conhecia e dominava muitos conhecimentos matemáticos e filosóficos da época. Através de estudos astronómicos, afirmava que o planeta Terra era esférico e suspenso no Espaço (ideia pouco conhecida na época). Encontrou uma certa ordem no universo, observando que as estrelas, assim como a Terra, girava ao redor do Sol
Recebeu muita influência científica e filosófica dos filósofos gregos Tales de Mileto, Anaximandro e Anaxímenes.
Enquanto visitava o Egipto, impressionado com as pirâmides, desenvolveu o famoso Teorema de Pitágoras. De acordo com este teorema é possível calcular o lado de um triângulo rectângulo, conhecendo os outros dois. Desta forma, ele conseguiu provar que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Atribui-se também a ele o desenvolvimento da tábua de multiplicação, o sistema decimal e as proporções aritméticas. A sua influência nos estudos futuros da Matemática foi enorme, pois foi um dos grandes construtores da base dos conhecimentos matemáticos, geométricos e filosóficos que temos actualmente.
Problema do Mês de Dezembro - 6 de dezembro de 2010Estrelinhas de Natal
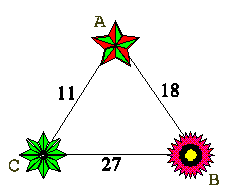
Por baixo de cada estrelinha de Natal estão três números escondidos. Em cada lado da árvore de Natal está a soma dos números secretos dos extremos. Quais são os números escondidos?
Escreve:
A=...
B=...
C=...
Solução do problema do mês de Outubro - 11 de novembro de 2010
A vida de um Matemático Português (Madeirense)... - 11 de novembro de 2010José Vicente Gonçalves (1896- 1985)

José Martins Vicente Gonçalves nasceu no Funchal em 26 de Agosto de 1896 e veio muito jovem para Coimbra, onde se licenciou com apenas 21 anos de idade. Foi logo contratado como 2º assistente do grupo de Mecânica e Astronomia da mesma universidade. O doutoramento trouxe-lhe a promoção a 1º assistente em 1921. A sua passagem a professor catedrático deu-se seis anos mais tarde, em 1927, depois de ter defendido outra dissertação, como era exigido na época.
Em 1942 Vicente Gonçalves transferiu-se para a Faculdade de Ciências de Lisboa onde ensinou até se jubilar, em 1966. No período de 1947 a 1960 ensinou igualmente no Instituto de Ciências Económicas e Financeiras, actual ISEG.
A contribuição científica de Vicente Gonçalves foi sobretudo importante em Álgebra e Análise clássicas, onde o matemático madeirense simplificou a demonstração de resultados conhecidos e obteve resultados inovadores.
Uma segunda vertente da contribuição de Vicente Gonçalves para as matemáticas nacionais foi o seu extenso trabalho pedagógico, como autor e como docente. Numa época em que abundavam, como ainda hoje abundam, as sebentas de má qualidade, Vicente Gonçalves dedicou grande cuidado à redacção de manuais escolares que primavam pelo rigor e organização.
A terceira grande contribuição de Vicente Gonçalves para a ciência portuguesa foi constituída pelos seus estudos históricos. Numa época em que pouco interesse havia pela análise do nosso passado intelectual, Vicente Gonçalves publicou uma série de minuciosos estudos sobre os trabalhos de alguns dos maiores matemáticos portugueses.
José Vicente Gonçalves faleceu a 2 de Agosto de 1985.
Curiosidade - 11 de novembro de 2010A Particularidade do Dígito 1
Um número composto só por algarismos 1 (num máximo de nove), quando elevado ao quadrado, proporciona um número capicua (simetria numérica perfeita). Confirma estes resultados com o auxílio da tua calculadora.
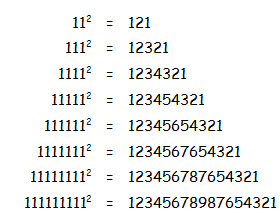
Problema do Mês de Novembro - 11 de novembro de 2010Frágil ponte
4 amigos pretendem atravessar uma frágil ponte de madeira. É noite, e é indispensável o uso de uma lanterna. A ponte somente suporta o peso de 2 pessoas e os amigos possuem apenas uma lanterna. Camila demora 8 minutos para atravessa-la, Manolito demora 4 minutos, Carlos demora 2 e Romerito 1 minuto.
Este percurso pode ser feito pelo 4 amigos em 15 minutos. Como?

Cálculos mentais - 28 de outubro de 2010Existem algumas técnicas interessantes e vantajosas para a realização de adições mentalmente. Porque não usá-las no nosso dia-a-dia?...

Problemas do Mês - Outubro - 28 de outubro de 2010Cinco cores e cinco números
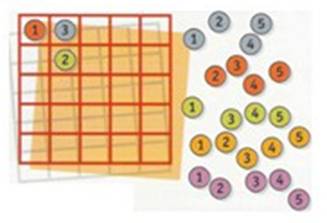
Temos fichas coloridas:
- 5 azuis;
- 5 vermelhas;
- 5 verdes;
- 5 cor de laranja;
- 5 roxas.
As cinco fichas de cada uma das cores estão numeradas de 1 a 5.
Como colocá-las num quadrado de 5 × 5 de tal modo que, em cada linha, em cada coluna e em cada diagonal principal não exista nenhuma cor repetida nem nenhum número repetido?
Nota: A solução será apresentada no mês de Novembro.
A vida de um Matemático... - 28 de outubro de 2010Thales de Mileto (624 a.C. - 546 a.C.)
Thales de Mileto foi um filósofo grego que nasceu na cidade de Mileto, na Jónia.
Muito pouco de preciso e certo se pode dizer acerca do pensamento de Thales. Não existe informação suficiente que nos permita afirmar se compôs alguma obra. No entanto, existem numerosas referências às descobertas que Thales efectuou.
O mérito de Thales de Mileto consiste em procurar explicações naturais dos fenómenos, sem recorrer a explicações míticas. Por este motivo, merece ser considerado o primeiro filósofo do Ocidente e que o seu nome conste em todas as listas antigas dos sete sábios da Grécia.
Thales foi o primeiro grego a estabelecer normas para o desenvolvimento da Geometria em termos abstractos, desvinculada de qualquer aplicação prática. É considerado o originador da organização dedutiva da Geometria, tendo contribuído para o início da Matemática como uma disciplina racional.
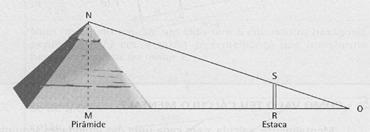
Diz-se que Thales se deslocou um dia ao Egipto, para calcular a altura da famosa pirâmide de Quéope e que, para tal, recorreu a uma vara, duas sombras e uma ideia.
Um sacerdote egípcio perguntou a Thales como procederia para calcular a altura da pirâmide de Quéope. Thales terá respondido:
"Espetava na areia esta ou outra estaca qualquer, cujo comprimento conhecesse, e media a sua sombra. Media também, à mesma hora, a sombra da pirâmide e adicionava-lhe metade do comprimento do lado da base. E pronto, em seguida saberia a altura da pirâmide".
|
|
 |
 |
|
 |
|